ホーム | 統計 Top | (応用)全日本吹奏楽コンクールの審査員を買収して確実に金賞を取る可能性を、モンテカルロ・シミュレーションで検討する
2015年5月15日初版
背景についてはこちらの記事を参照のこと。
目次
- 前提:吹奏楽コンクールの審査内規など
- 審判を買収してどのような不正行為を行うのか?
- アルゴリズム
- 各出場団体の「実力」を「(評価)順位」に変換する処理
- 各団体の「順位」から「ABC評定」への変換
- ABC評定から賞を決定する処理
- 買収された審査員による評価操作
- シミュレーション実行用のRソースコード
- シミュレーション本番
- シミュレーション 1(審査の不確実性がゼロのとき)
- シミュレーション 2(審査に若干の不確実性があるとき)
- シミュレーション 3(審査にある程度の不確実性があるとき)
- シミュレーション 4(審査に大きな不確実性があるとき)
- シミュレーション結果の解釈
- 結論
前提:吹奏楽コンクールの審査内規など
2013年の暮れにこちらの前回記事で、吹奏楽コンクールの新しい審査方法において、金・銀・銅賞比率がどのようになるかを予測した。ちなみに2014年全国大会の審査結果だが
中学前半(15団体)では金5銀5銅5
中学後半(14団体)では金5銀7銅2
高校前半(15団体)では金4銀7銅4
中学後半(14団体)では金4銀7銅3
となっている。心なしか後半の銅賞出現率が低いようにも見える。ただし銅賞(1)か否(0)かという事象の生起に、前後半が与える影響を、二項分布を仮定した一般化線形モデルで調べたところ、AIC=66.9(前後半を考慮) vs 66.1(ヌルモデル) であった。要するに2014年度の結果だけでは、前後半の影響が有るとも無いとも言い切れないボーダーライン上だ。
そして吹連は(わたしの前回記事を読んだわけではなかろうが)2015年度全国大会から中学、高校の部の後半出場団体数を1団体ずつ増やす方針を打ち出しており、前後半とも各15団体で争うことになる(出典:全日本吹奏楽連盟会報「すいそうがく」197号)。従って、前後半の間で審査基準が不公平に作用するリスクは、当面回避されたと言えるだろう。
さて、前回の記事では「ルール上の不公平性」について問題提起したわけだ。今回は一歩進んで、この吹奏楽コンクールの審査システムが不正行為、具体的には審査員の買収に対してどの程度頑健であるか (robustness) を検証したい。例によって、まずは考察の前提となる審査内規を示しておく。
全日本吹奏楽連盟会報「すいそうがく」194号より
(2015年以降の審査に関係すると思われる項目を抜粋。下記を含む「第3号議案」の全体は前回記事に引用している)
///////////ここから引用(著作権法第32条に基づく研究目的での引用)
1. すべての事業の審査は総合的に評価し「A(金)・B(銀)・C(銅)」の3段階で行う。「A・B・C」の個数については審査説明会で示し、審査員に厳守してもらう。なお、点数化は行なわない。
2. 賞は、審査員の過半数以上がA評価...金賞
過半数以上がC評価...銅賞
それ以外...銀賞
3. 審査結果が次の場合も認める。
・ある賞が、「ゼロおよび1」となった場合。
・部門および前後半での「賞の数がアンバランス」となった場合。
II. 上記を受けて、審査員に付けてもらう各事業のA・B・Cの個数は次のとおりとする。
原則
3で割り切れる団体数の場合は、A・B・C同数とする。
3で割った場合に端数が1出る場合は、Aを+1とする。
3で割った場合に端数が2出る場合は、AとBを各+1とする。
(例)コンクール中学・高校の部
前半の部は15団体なので、A:B:Cは5:5:5
////////// ここまで引用
(すぐ上で「前半の部は15団体」と書いてあるが、2015年以降は後半も15団体になる予定)
補足:中学および高校の部では審査員は9人いる。各審査員は順位に応じて、自分が持っている規定数のABCを各演奏団体に配分し、この集計結果に応じて賞が決定する。上下カットの有無は明言されていないため、行わないものと仮定する。
審判を買収してどのような不正行為を行うのか?
具体的なシチュエーションとして、「出場団体のうち1組(以下、団体甲とする)が、審査員のうち1名(以下、審査員乙とする)に極秘裏に接触し、その審査員の裁量範囲内で甲の評価を高めるための操作を依頼する」場合を考える。ただし甲乙以外の全ての出場団体、審査員および大会主催者は、自ら買収に関与せず、この大会で買収行為が行われていることも一切関知しないものとする。
もちろん、甲が乙に対して依頼するであろう操作は以下である。
- 操作: 団体甲の評定を、演奏の巧拙に関わらずAとする
おそらくこの程度の操作で、乙に疑惑の目が向けられることは無いだろう。だが審査員は9人いる。一人がAを付けたからといって即金賞になるわけではない。次節では、この不正操作の模様をRでシミュレートするためのアルゴリズムを説明する。
アルゴリズム
前の記事からパーツを流用していますが、審査員のインチキ操作に関する計算手順を追加しています。
各出場団体の「実力」を「(評価)順位」に変換する処理
たとえば15出場団体のそれぞれが「真の実力値」を有しており、これらが平均0、標準偏差1の正規分布に従うと仮定。
# それぞれの団体の真の実力値を
realpoint <- rnorm( 15, mean = 0, sd=1 )
# さらに、「評価の不確実性」を加味
estimated <- realpoint + rnorm(15, mean=0, sd=x)
(原理)平均0、標準偏差xの正規分布に従って、各団体の実力がランダムに、審査員によってoverestimate(ないしunderestimate)される。
このとき変数xで定義されている正規分布の標準偏差が、評価の不確実性の強さを表す。
各団体の真の実力値を審査員が完璧に計れるなら、標準偏差はゼロにできるだろうし、非常に評価が割れやすいならば標準偏差は大きな値を取るだろう(つまり審査結果は完全なランダムに近くなる)。
このestimatedが、不確実性の加味された審査結果である。これを、数値が大きい順に1から15まで番号を割り振ることにより、各団体の「順位」に換算できる。
# 各団体の順位に換算
rank <- rank(-estimated) # estimatedは長さ9の数値ベクトル
##なおRのrank()関数の定義により、値が小さいほうから順に順位が付けられるため、マイナスを付けて渡している
真の実力値は大会ごとに固定だが、審査員は9人いるから、上記のうち審査の過程のみを9回独立に行い、個別のデータに格納しておけばよい。
各団体の「順位」から「ABC評定」への変換(正しい審査員の場合)
ABC評定処理を、以下のようにRの関数として定義しておく。
# 各審査員が付ける評価。引数 x は順位を表すスカラー
# たとえばn.band=15として、xの値が1–5でA、6–10でB、11–15でCとなる。
makeABC <- function (x) {
if ( x <= num.A ) {
return( as.character("A") )
} else if ( x <= num.A+num.B ) {
return( as.character("B") )
} else {
return( as.character("C") )
}
}
買収された審査員による評価操作
ここで、1人の審査員(乙)が評価を不正に操作して返すものとする。乙が行う処理は、上記の順位換算までは正しい審査員と同じだが、その後ABC評定が恣意的に操作される。Rによる処理は少し長くなるので、下のシミュレーション本番用ソースを参照のこと。
ABC評定から賞を決定する処理
ここからは、審査員から渡されたABC評定を元に、大会主催者が計算を行う。審査員1から8までは正しく審査をしており、9番目の審査員である乙が評価を操作しているが、大会主催者は不正の事実を知らないものとする。
2. 賞は、審査員の過半数以上がA評価...金賞
過半数以上がC評価...銅賞
それ以外...銀賞
# 賞の判定も関数として定義しておく。
# 長さ n.judge の文字列ベクトル(ある団体への評価を"A","B","C"などとして並べたもの)を引数に取る。
hantei.char <- function (x) {
if ( length(grep("A", x))*2 > length(x) ) {
return( as.character("gold") )
} else if ( length(grep("C", x))*2 > length(x) ) {
return( as.character("copper") )
} else {
return( as.character("silver") )
}
}
# こちらは判定を数値で返す
hantei <- function (x) {
if ( length(grep("A", x))*2 > length(x) ) {
return( as.numeric(1) )
} else if ( length(grep("C", x))*2 > length(x) ) {
return( as.numeric(-1) )
} else {
return( as.numeric(0) )
}
}
シミュレーション実行用のRソースコード
以下の関数を定義してぶん回す。すぐ上にある makeABC(), hantei() のサブルーチンも内部で改めて定義したので、準備としてはこの下の85行分を一括選択してRコンソールにペーストするだけ。
# 関数の定義
# デフォルト値はバンドの数15、審査員数9、審査の不確実性における標準偏差1, 繰り返し回数1000
iterate <- function (n.band=15, n.judge=9, deviation=1, TIME=1000, char=TRUE ) {
# 審査員がつけるABCの個数。団体数の1/3を基本に、割り切れない時はA,ついでBを増やす。
num.A <- n.band %/% 3 + ceiling( (n.band%%3)/2 ) # 0.5ないし1で、1を返させる
num.B <- n.band %/% 3 + floor( (n.band%%3)/2 ) # 0.5で0, 1で、1を返させる
num.C <- n.band %/% 3
# 各審査員が付ける評価。xは順位を表すスカラー
# たとえばn.band=15として、xの値が1–5でA、6–10でB、11–15でCとなる。
makeABC <- function (x) {
if ( x <= num.A ) {
return( as.character("A") )
} else if ( x <= num.A+num.B ) {
return( as.character("B") )
} else {
return( as.character("C") )
}
}
# 賞の判定も関数として定義しておく。文字列ベクトルを引数に取る。
hantei.char <- function (x) {
if ( length(grep("A", x))*2 > length(x) ) {
return( as.character("gold") )
} else if ( length(grep("C", x))*2 > length(x) ) {
return( as.character("copper") )
} else {
return( as.character("silver") )
}
}
# こちらは判定を数値で返す
hantei <- function (x) {
if ( length(grep("A", x))*2 > length(x) ) {
return( as.numeric(1) )
} else if ( length(grep("C", x))*2 > length(x) ) {
return( as.numeric(-1) )
} else {
return( as.numeric(0) )
}
}
award.true.matr <- matrix(numeric(n.band*TIME), nrow=n.band, byrow=F)
award.alter.matr <- award.true.matr
for(i in 1:TIME) {
# 点数データ
data.matr <- matrix(numeric( n.band*n.judge ), ncol=n.judge, byrow=F)
# 15出場団体の真の実力値を作成し格納。実力のばらつきはsd=1に固定。
# 実力点数が高い順に整列させておく(ここでは出場順は関係ないので)。
raw.vect <- sort(rnorm( n.band, mean=0, sd=1 ), decreasing=TRUE)
# データの2:10列目に、審査員9人が全員正直に審査した場合の各団体に付く素の評価を格納。
data.matr[1:(n.band*n.judge)] <- rep(raw.vect, n.judge) + rnorm( n.band*n.judge, mean=0, sd=deviation )
# 各審査員によって付けられる順位データ
# 蛇足:Rのrank()関数の定義により、値が小さいほうから順位が付けられるため、マイナスを付けて渡している
rank.matr <- apply( -data.matr, MARGIN=2, rank )
abc.matr <- apply( rank.matr, MARGIN=c(1,2), makeABC )
#賞を判定
# 1行目から15行目まで、各出場団体をそれぞれ表す
# 1列目から9列目までが審査員9人による、素直な採点結果のABC評定
if(char==TRUE) {
award.true.vect <- apply( abc.matr, MARGIN=1, hantei.char )
} else {
award.true.vect <- apply( abc.matr, MARGIN=1, hantei )
}
award.true.matr[, i] <- award.true.vect
# 次に、不正操作ありの場合。
# abc.matrを元データに使う。このうち不正に関与する審査員乙は、常に最後の人(データn.band列目)であるとする。
# 不正を依頼した団体甲は、データ x 行目(実力が x 番目に高い事も指す)に位置するものとする。
alter.abc <- abc.matr
alter.abc[, n.judge] <- "A"
if(char==TRUE) {
award.alter.vect <- apply( alter.abc, MARGIN=1, hantei.char )
} else {
award.alter.vect <- apply( alter.abc, MARGIN=1, hantei )
}
award.alter.matr[, i] <- award.alter.vect
}
return(list(true=award.true.matr, alter=award.alter.matr))
}
# ここまでをコピペして関数定義
シミュレーション本番
さっそく、繰り返し回数100,000回としてシミュレーションを回す。つまり、この審査内規に従って吹奏楽コンクールを10万年間やり続けた結果ですね。
シミュレーション 1(審査の不確実性 = standard deviation がゼロのとき)
まず審査の不確実性がゼロ、つまり真の実力がそのまま、前後半それぞれの出場団体の評価順位に反映される場合をシミュレートする。
# SD=0
n.band <- 15
n.judge <- 9
TIME <- 100000
deviation <- 0
result <- iterate(n.band=n.band, n.judge=n.judge, deviation=deviation, TIME=TIME, char=TRUE)
change.matr <- matrix(rep("nc", n.band*TIME), nrow=n.band)
for (i in 1:(n.band*TIME) ) {
if(result$true[i] == "gold" && result$alter[i] == "gold") {
change.matr[i] <- "gg"
} else if(result$true[i] == "silver" && result$alter[i] == "gold") {
change.matr[i] <- "sg"
} else if (result$true[i] == "copper" && result$alter[i] == "gold") {
change.matr[i] <- "cg"
} else if (result$true[i] == "silver" && result$alter[i] == "silver") {
change.matr[i] <- "ss"
} else if (result$true[i] == "copper" && result$alter[i] == "silver") {
change.matr[i] <- "cs"
} else if (result$true[i] == "copper" && result$alter[i] == "copper") {
change.matr[i] <- "cc"
}
}
cross.change <- matrix(numeric(6*n.band), nrow=6) # 操作後の結果別
for (i in 1:n.band) {
x <- change.matr[i,]
cross.change[, i] <- c(length(grep("gg",x)) , length(grep("sg",x)), length(grep("cg",x)) , length(grep("ss",x)) , length(grep("cs",x)), length(grep("cc",x)) )
}
cross.change_0 <- cross.change# 他のオブジェクトと異なる名前で代入しておく
# 計算できたので結果を表示
barplot( cross.change_0, beside=F )
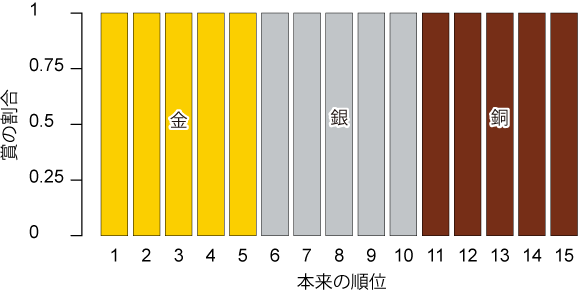
Fig. 1 | 審査に不確実性が無いとき(SD=0)の、審査員買収の効果。横軸は、不正を依頼した演奏団体の本来の実力が、全15団体中の何位に相当するか。縦軸は、不正込みの審査結果において、その団体が得た賞(100,000回の試行で得られた賞の割合)。
審査に不確実性がない場合に買収操作を行っても、上位の賞を取れる可能性はまず上がらないことが見て取れる(10万回の試行において、順位変動は1回も現れず)。審査員団が演奏団体の実力について一致した見解に至るならば、うち1人がそれに反して評定を吊り上げたところで、他8人の評定を覆せないのであろう。
シミュレーション 2~4(SD = {0.1, 1, 10} の各場合)
# シミュレーション実施手順は省略
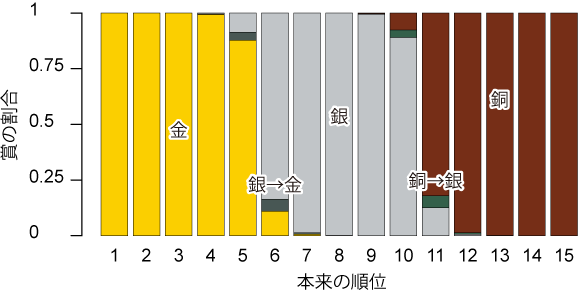
Fig. 2 | 審査に若干の不確実性があるとき(SD=0.1)の、審査員買収の効果。「銀→金」は、本来は銀賞相当だが買収の結果、金賞になったことを表す。「銅→銀」も同様。
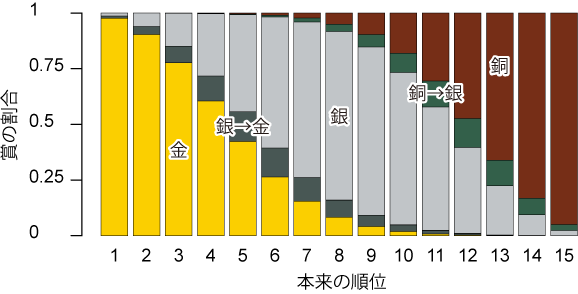
Fig. 3 | 審査にそれなりの不確実性があるとき(SD=1)の、審査員買収の効果。
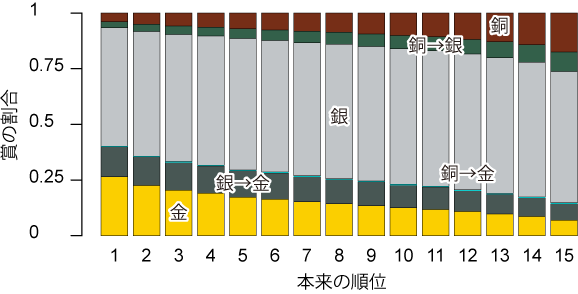
Fig. 4 | 審査に大きな不確実性があるとき(SD=10)の、審査員買収の効果。
つまり、審査に大きな不確実性があるとき、まず審査結果そのものが本来の実力を反映しなくなる。このとき、買収されて無理やりA評定を付ける審査員が1名でも現れると、その影響で賞が上がる事態がそれなりの蓋然性で起こる。
シミュレーション結果の解釈
- 審査の不確実性が小さく、誰が聴いても各演奏団体の実力について一致した見解に至るならば、審査員の1人を買収したところで実力以上の賞を取れる可能性は低い。
- 審査の不確実性が増し、審査員間での評価が割れるほど、(前回記事で書いたとおり)コンクール全体としては金賞および銅賞受賞率が低くなり、銀賞が増える。このとき、買収操作を行った団体が実力以上の賞を取れる可能性は、ある程度高まる。
- 本来の実力が賞のボーダーライン近くにあるほど、買収によって上の賞を取れる可能性は高まる。ただしそれなりの蓋然性で上位入賞できるのは、審査の不確実性がきわめて高い(全団体の実力が拮抗していたり、あるいは審査員各人の趣味嗜好がバラバラだったりするような)場合に限られるだろう。
結論
倫理的にはアレだが、吹奏楽コンクールにおいて毎年金賞と銀賞、あるいは銀賞と銅賞の間をフラフラ彷徨っている団体であれば、審査員への買収工作はまんざら無駄とも言い切れない。しかし9人中1人の買収では、確実に上位入賞することもまた、難しいだろう。
蛇足
そうなると読者の諸兄姉方が気にするであろうことは、実際のコンクールにおいて「審査の不確実性」がどの程度の大きさなのか、と言う点であろう。残念なことに、一般に公開されている情報から知るのは極めて困難だ。原理的には「それぞれの団体に対する、審査員間でのABC評定の割れ具合」が分かれば、モデルを立てて点推定することは可能だと思う。しかし、吹連は2014年からABC評定のデータを公表しなくなってしまった。だから、この話はここでお終いなんだ。